[Resuelto] Prototipo de un cohete
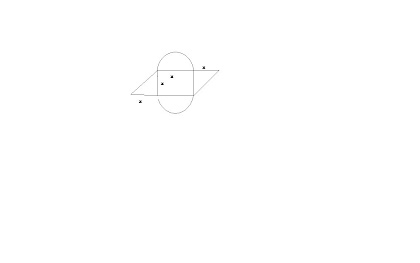
Efrain esta fabricando una pieza que se usara como base para el lanzamiento de uin prototipo de cohete.Esta esta formada por dos regiones en forma de triangulo isoceles, como muestra la figura. El diametro de los semicirculos es X al igual que los dlados iguales de los triangulos.
Efrain usara una lamina de titanio para la fabricacion pero quiere encontrar primero una expresion en funcion de x para el area total que ocupara la lamina y con ella calcular tanto la cantidad de material que gastara como el costo del mismo.
1. Teniendo en cuenta que el area de un circulo es igual a: πr2, entonces el area A en funcion de x, que encontrara Efrain para su diseño se puede expresar como:
A. A(x): x2 (2+π/4)
B. A(x): x (π/2+2x)
C. A(x): πx2
D. A(x): 2π + πx2
2. Si Efrain pone un almabre alrededor de su diseño para reforzarlo, de forma tal que encierre completamnete el perimetro de este. la funcion en terminos de x que permite determinar dicho permitro puede ser:
A. P(x): 2πX + x√2 + x
B. P(x): 2 (πx + x√2 + x)
C. P(x): πx2 + 2√x +2
D. P(x): x ( π+2 + √2 )
Pregunta enviada por Michelle
Efrain usara una lamina de titanio para la fabricacion pero quiere encontrar primero una expresion en funcion de x para el area total que ocupara la lamina y con ella calcular tanto la cantidad de material que gastara como el costo del mismo.
1. Teniendo en cuenta que el area de un circulo es igual a: πr2, entonces el area A en funcion de x, que encontrara Efrain para su diseño se puede expresar como:
A. A(x): x2 (2+π/4)
B. A(x): x (π/2+2x)
C. A(x): πx2
D. A(x): 2π + πx2
2. Si Efrain pone un almabre alrededor de su diseño para reforzarlo, de forma tal que encierre completamnete el perimetro de este. la funcion en terminos de x que permite determinar dicho permitro puede ser:
A. P(x): 2πX + x√2 + x
B. P(x): 2 (πx + x√2 + x)
C. P(x): πx2 + 2√x +2
D. P(x): x ( π+2 + √2 )
Pregunta enviada por Michelle


|
Publicado por
Felipe Calvo
Ingeniero Industrial y Magíster en Estadística de la Universidad Nacional de Colombia. Consultor en políticas públicas y docente universitario. Conoce más de mi trabajo. Instagram: Felipe CalvoTwitter: @feliperspicuo |

whatshot Lo Más Popular
- Puntajes de admisión para cada carrera de la Universidad Nacional de Colombia
- Zona Interactiva: Exámenes online preparatorios para el Icfes Saber 11 y el examen de admisión de la Universidad Nacional
- Calcular promedios del examen Icfes Saber 11
- Examen de Estado ICFES - Mini Cuestionario Interactivo
- Examen de estado Icfes Saber 11: Interpretación de Resultados
bookmark_border Artículos Destacados
Pasar a la Universidad Nacional
12 Consejos para el Examen
¡Consulta tu carrera!
Consejos y Tips Examen Icfes Saber 11
¿Qué estudiar? ¿Qué repasar?
Interpretar Resultados ICFES
Calcular Promedios ICFES
Puntajes de Admisión UNAL
Estructuras y respuestas exámenes de admisión UNAL
Inscripciones ICFES y UN: paso a paso
Preguntas Frecuentes ICFES y UN
12 Consejos para el Examen
¡Consulta tu carrera!
Consejos y Tips Examen Icfes Saber 11
¿Qué estudiar? ¿Qué repasar?
Interpretar Resultados ICFES
Calcular Promedios ICFES
Puntajes de Admisión UNAL
Estructuras y respuestas exámenes de admisión UNAL
Inscripciones ICFES y UN: paso a paso
Preguntas Frecuentes ICFES y UN
forum Últimos Comentarios
person_add En Contacto
¿Deseas ponerte en contacto con nosotros?
Escribe al correo electrónico elblogdelanacho[arroba]gmail.com o contáctame a través de Instagram.


Estas son de esas preguntas que odiarías que te salieran en el Icfes, voy a investigar un poco porque la verdad no entiendo ni fa de ninguna de las dos.
Saludos. Carlos Sz. |O
no entiendo alguien me explica?
holas
bueno que pregunta mas interesante esta :D
haré el primero supongo me dio la respuesta aunque tengo mis dudas..
haber tenemos un prototipo que consta de un paralelogramo y dos semicirculos o un circulo
el A paralelogramo es b*h la base es 2x la altura es x
A= 2x²
ahora el circulo el radio es x/2
π(x/2)²
π(x²/4)
por lo tanto tenemos
2x² + π(x²/4)
x² + π(x²/2)
ahora simplificando a x tenemos
x ( x + π(x/2))
x (2x+ π/2)
bueno eso seria entonces para el inciso B... nuevamente digo no estoy muy seguro juzguen y opinen saludos :D mas tarde paso a ver la otra
Danny si, eso es lo que yo mas o menos habia hecho pero no me habia salido, tambien creo que esa puede ser la respuesta.
Ahora la cosa es hacer la segunda que esta un toque mas complicada, ahi miro que logro sacar.
Carlos Sz. 8)
no lo había visto así, me inclino por la A
Bueno yo lo veo así:
Dice que son dos semicírculos y dos triángulos isósceles así que el cuadrado se va!
decimos que el área de un semicírculo + otro semicírculo + un triangulo + otro triangulo = área total
πx2/2 + πx2/2 +x2/2 +x2/2 = área total
factor común x2
x2 ( π/2 * π/2 + 1/2 +1/2)
x2 ( π/4 + 2 )
respuesta A
En la 2 es el perímetro por lo que se hallan la hipotenusa y la circunferencia del circulo
entonces : πx + 2x + la hipotenusa de los triángulos que es x√2
listo
πx + 2x + x√2
factor común :x
x (π + 2 + √2)
D
Diría que es así. Adios
Michelle ♥
al que quiera tengo otra pregunta referente a ese mismo punto
3. Efrain decide fabricar la pieza sin tener en cuenta las zonas semicirculares. Considerando que el metro cuadrado de titanio le cuesta $ (Px - 10 ), la pieza a fabricar le costara
A 2x2(P -10)
B 2x3 P-10x2
C x2 -(2P -20 )
D 2x3P -20x2